Math Journey 5:
The Pronic Numbers
“Uncle Bob” Mead
Part 1: Pronics Among the Whole Numbers | Part 2: Sums of the Pronic Numbers and Geometric Models
Part 3: Pronic Reciprocals and Pronic Doubles: An Equation Mis-Pelled | Part 4: Pronics and Primes Awhirl
2
4 6
8 10 12
14 16 18 20
22 24 26 28 30
32 34 36 38 40 42
44 46 48 50 52 54 56
…
The Even Triangle
This journey will focus on the infinite set {2, 6, 12, 20, 30, 42, …}, the pronic numbers, found running down the right edge of the triangular formation of even numbers above. The set has many connections among numbers and geometric models, and I was pleased to stumble on a fresh way to look at them, the Sacks Spiral – it’s the wish for anyone on a journey, right?
Introduction
Right from the start we have a name problem – or several. I’ve had students in high school and college investigate these numbers, but I never referred to them as pronic numbers. Problem One: The descriptor has no “sizzle,” and as a matter of fact I rate it nerd-plus. Problem Two: Pronic seems to be a misspelling. Problem Three: As many of you know, the subject of mathematics demands precision in its statements, and especially in the definitions of terms. “Pronic” just isn’t precise.
Eric Weisstein of Wolfram explains. “Pronic numbers are also known as oblong (Merzbach and Boyer 1991, p. 50) or heteromecic numbers. However, "pronic" seems to be a misspelling of "promic" (from the Greek promekes, meaning rectangular, oblate, or oblong). However, no less an authority than Euler himself used the term "pronic," so attempting to "correct" it at this late date seems inadvisable.”
[Pronic Number." From MathWorld — A Wolfram Web Resource]
Pronic numbers are the products of two counting numbers that differ by one. There! A concise, precise definition, and the first few examples are: 1 * 2, 2 * 3, 3 * 4, 4 * 5, and so on. I once used the term “oblong” for these, but that term encompasses all non-square rectangles. A 3x5 rectangle is an oblong and 15 is a non-square product, but they are outside of our topic. In our journey, the pronics are nearly square, and if you looked at a drawing of a rectangle that measured 83 by 84 millimeters, it would appear square to you, right? Question for you: Why are the pronic numbers all even?
But what good are they? … the pronics, that is. Here is a little poser, the solution to which employs some of the pronic properties we expose in Part One below.
The Meade School of North Philadelphia had budgeted $702.00 for its field trip to the Franklin and other points downtown. Each student was assessed an equal share of the cost, but just one week before the trip, one student moved away. Fortunately, it was calculated that just one extra dollar per student would cover the full cost. How many students went on the trip?
Part One
Pronics Among the Whole Numbers
“Do you know your times?” is a very common question among the grade school set. Some of the multiplication facts include square and pronic products. In the diagram at right, you can see the square numbers 1, 4, 9, 16, … running down the main diagonal, and running in the same direction just above and just below the squares are the pronic products, one sequence marked with an oblong block.
Narrowing our focus to just the 5 by 5 portion upper left in the table, the squares max out at 25 and the pronics at 20. Above the squares there is a triangle of entries consisting of the four pronics 2, 6, 12, and 20, topped by 3, 8, and 15, then 4 and 10, and finally 5 in the upper right corner. Due to the symmetry of the chart, those same products make up a triangle below the squares. The counts of products in both triangles is 10 + 10, and that equals 20, our highest pronic in the square. Is that just a coincidence? Let’s look at another triangular formation.

x 1
x x 3 = 1 + 2
x x x 6 = 1 + 2 + 3
x x x x 10 = 1 + 2 + 3 + 4
x x x x x 15 = 1 + 2 + 3 + 4 + 5
… …
Ten is part of a set of triangular numbers. They have the property of being the sum of the counting sequence (1 + 2 + 3 + 4 + …), up to a certain maximum.
The formula that gives triangular sums will lead us to a formula for pronics. The sum of {1, 2, 3, 4} is half of the sum of {1, 2, 3, 4} and {4, 3, 2, 1}. If we pair those up in order and sum we get (1 + 4), (2 + 3), …, or four pairs of 5. So the triangular sum is half of 4*5 or ten. Note that 4*5 is our pronic number 20. Formulas need to work for any size triangle, so let’s get the sum for the set {1, 2, 3, 4, …, n}. We. again sum this set with a reversed duplicate.
1 2 3 4 … n
n n-1 n-2 n-3… 1
We get n pairs each with a sum (n + 1). So our triangular number is n*(n + 1)/2, and more to the point, our pronic formula is n*(n + 1), precisely how they were defined. More on the triangular connection in Part Two of our journey.
Expanding the list. There is no limit to the set of whole numbers, and so the set of pronics is infinite as well. Lots more of them to play with; here are more.
{2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380, 420, 462, …}
Let’s use the function symbol Pr(n) for the nth pronic in the list. The formula becomes Pr(n) = n*(n + 1), and we have found that Pr(4), the fourth pronic, is 4*5 or 20. So Pr(15) = 240 because 240 equals 15*16. We now have two reasons that pronics are all even. They are the double of triangular numbers, and they are the product of an even and an odd number.
Another shape connection. There is a square number exactly half way between consecutive pronics. The mean of 20 and 30 is 25, a square. The mean of Pr(14) and Pr(15) is (210 + 240) /2 or 225, the square of 15. A little algebra shows that this relationship holds for the entire set.
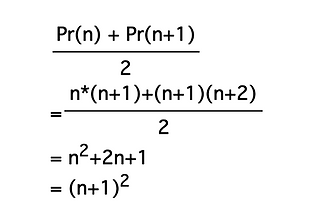

So square numbers are always midway between two consecutive pronics. The shoe on the other foot says that each pronic number lies between two consecutive squares, just as 90 (9*10) lies between the squares 81 and 100, and just a half unit away from their mean of 90.5. At the left we show that this is always the case.
At the top of this journey we depicted the pronic products on one edge of a triangle of even numbers. We follow with a second triangular model.
The Even Series Triangle
In this model we find the pronics by summing each row. We are doubling up on the model for triangular numbers. Pronics are an accumulation of consecutive even numbers. What is the sum of all even numbers 2 through 100?
2 = 2
6 = 2 + 4
12 = 2 + 4 + 6
20 = 2 + 4 + 6 + 8
30 = 2 + 4 + 6 + 8 + 10
…
A Test for Pronic Numbers
The fact that there is a pronic between consecutive squares allows us to test any number for membership in the set. Is 92 a pronic number? We find its square root to be 9.59 approximately. So 92 lies between the squares of 9 and 10, but 9*10 is not 92. Pick a number at random: is 3,987,554 a pronic number? The square root is 1996.89. We check 1996*1997 which is 3,986,012 and that product is the only pronic in the neighborhood.
Solution to the Meade School Field Trip poser: The full cost $702 is a pronic number, wouldn’t you know. Originally there must have been n students paying x dollars each. But (n – 1) students were charged an extra dollar. Do we need to set up and solve an equation? Nah! To find the factors of 702 that differ by one, simply take the square root: 26.5. So 26 students went on the trip each paying $27.
Part Two
Sums of the Pronic Numbers and Geometric Models
{2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380, 420, 462, …}
In Part One of our Journey we defined a pronic number as the product of two consecutive counting numbers. You can see a partial list above. We established that there is a square number between successive pronic numbers, for example 16, falling between 12 and 20. The flip side of this is also true: that there is one pronic between successive squares. Pronics and squares play leap frog all the way to infinity. What is the pronic number between 7-squared and 8-squared?
I was very pleased to have made a fresh discovery as I ambled along in this topic. As recently as 2003 software engineer Robert Sacks published a new way to chart the whole numbers. He placed them in a spiral running counterclockwise from zero in the center to each square number on the right, the easterly direction, so that between 1 and 4, the spiral makes space for 2 and 3, and between 4 and 9, the spiral spaces 5, 6, 7, and 8. We’ll see many features of this charting method further along, but for now we merely note that the spiral conveniently locates all the pronic numbers in a westerly direction.

25 + 100*Pr(n) is a square!
Here we have another pronic/square connection: if you tack the digits 25 onto the end of a pronic, it becomes a square number. A simple one to see is 25 appended to the pronic 6, and 625 is the square of 25. Appending 25 onto Pr(15), that’s 25+100*240, we have 24025. You might want to warm up the square root key on your calculator app to see that 24025 is also a square number. A few steps of algebra will take 25+100*n*(n+1) to the expression confirming a square number.
Pronic Numbers and Triangles
On May 2 this year, our grocery receipt reported that we saved $20.56 buying items that were on sale, and we saved $399.40 so far in 2024. So the almost $400 constituted a running total, an accumulation of the savings in the year to date. We now consider what the numbers look like when we accumulate the pronic numbers, and our path takes us through the triangular numbers again [see more in Part One].
In one seven-inning softball game, the Teaneck Tigers amassed a passel of runs. The scoreboard showed the runs scored for each inning: 1, 2, 3, 4, 5, 6, 7. That’s right. In each inning they scored one more run than in the previous one. So after two innings they had 3 runs total, and after three innings a total of 6. These are the running totals, and they amount to the triangular sequence 1, 3, 6, 10, 15, 21, and 28 for this game. The sequence is called triangular because it can be modeled as below.

The sequence counts the nodes in our model as more rows are added without limit. We established in Part One that the pronic numbers amount to twice the triangular ones. So the pronic sequence can be modeled by two triangles, one inverted, joined at their apexes. The pronic sequence is extended by growing the model both at the top and at the bottom, as at the right.
Sums of the Pronic Numbers
What would a running total of the pronic numbers look like? The sequence would begin with 2, then 2 + 6, 2 + 6 + 12, and so on, but these are just doubles of…


Again we start with the triangular sequence and find their sums: 1, 1+3, 1+3+6, 1+3+6+10 and so on. This sequence {1, 4, 10, 20, 35, …} is known as the tetrahedral sequence and, would you believe, we can find it in our multiplication table!
The square numbers are in a diagonal running northwest to southeast, and adding those products gives the sum of squares from one to any limit. The products in diagonals going the other direction, i.e. northeast to southwest, can be summed to give the tetrahedral sequence, e.g., 3, 4, and 3 make 10 in the third of those diagonals; the third tetrahedral number is 10. A tetrahedral shape is a pyramid with a triangular base, so tetrahedral numbers are built from sums of triangular numbers. See below.
We accompany this sequence with a Person X singing “On the first day of Christmas my true love gave to me ….”
The gift types and amounts given to Person X in the Christmas carol are one partridge, two turtle doves, three French hens, four calling birds, five gold rings, on up to 12 something or others. The gifts total much more than 1 + 2 + 3 etc. because all the previous gifts are given again each day. The total gifts given after two days is 1 + 3 or 4: a partridge, two turtle doves, and another blessed partridge. Result: 12 partridges (one each day), 22 doves (2 for each of 11 days), etc., etc.! You’ll find these subtotals marked with a G in the multiplication table. What do the Gs add up to?
The running totals are given by summing the triangular sequence:
1, 1 + 3, 1 + 3 + 6, and so on.

Person Y with Two True Loves
On the first day each of the loves dropped off a partridge. How many gifts is person Y accumulating?
The partial sum sequence is double Person X’s haul: {2, 2+6, 2+6+12, 2+6+12+20, 2+6+12+20+30 …}, which means we are accumulating the pronic numbers.
This sequence begins {2, 8, 20, 40, 70 …}, again all even numbers, and twice
the running totals of the tetrahedral numbers, so our fanciful model is …

... which can be extended at the top and the bottom. Each duplicated tier adds the next pronic, and the running totals top and bottom combined are 2, 8, 20, 40, 70, and so on.
The sum of all the pronics is infinite. The sum of the first k pronics, that is, the sum from 2 through k*(k + 1), is given by
[k*(k + 1)*(k + 2)]/3
For example the third pronic sum, when k = 3, is 3*4*5/3 or 20. This formula doubles the tetrahedral sums sequence.
Sources:
Pronics as figurates
Sack’s spiral
Next month, in part 3, we reciprocate with pronic reciprocals, and we double down with double pronic numbers. See ya!
Part Three
Pronic Reciprocals and Pronic Doubles
For quick reference we repeat the first 21 pronic numbers. They are the products of two consecutive counting numbers. [see Parts One and Two above]
{2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380, 420, 462, …}
Sum of Pronic Reciprocals: Up Telescope!
In mathematics, telescoping series are sums that are less than what meets the eye. For example, if we want to know the sum of the halving series below, we could muck around with a common denominator or smartly convert it into a collapsing series.
S = 1 + 1/2 + 1/4 + 1/8 + 1/16
S = 1 + (1 – 1/2) + (1/2 – 1/4) + (1/4 – 1/8) + (1/8 – 1/16)
S = 1 + 1 – (1/16)
S = 1 + (15/16)
The terms involving 1/2, 1/4, and 1/8 collapsed to zero. Down telescope! This trick is used to show that the sum of reciprocals of 1, 2, 4, 8, 16, 32, 64, … without limit reaches just 2 as a limit.
What would be the sums of reciprocals of pronic numbers? Let’s take the first five and get a partial sum. We use the clever telescoping trick once more.
T = 1/2 + 1/6 + 1/12 + 1/20 + 1/30
T = 1/2 + (1/2 –1/3) + (1/3 – 1/4) + (1/4 – 1/5) + (1/5 – 1/6)
T = 1/2 + (1/2) – (1/6)
T = 1 – (1/6), the difference between one and the last reciprocal in the sum.
Recall that our function notation Pr(n) means that Pr(1000) = 1000*1001. By the pattern above we see that the sum of 1/2 through 1/Pr(1000) is 1 – (1/10001000), or one minus a hair. We use a limit argument to say that the reciprocals of all the positive pronics sum to just one.
Pronic Doubles of Pronic Numbers
In asking my next set of questions I innocently made this journey richer by half, and gave myself a couple of days work reviewing topics from algebra and number theory. We have established that the pronic numbers are all even, but scanning the list at the top, I noticed that some pronics were the doubles of others. Well, two pairs anyway: 6 and 12, and 210 and 420. This begs some compelling questions:
1. Are there more examples further “up” the list?
2. How can I locate them efficiently – could they be scarce and huge numbers?
3. Are there an infinite number of double pronic numbers?
4. What does it take to get into this club? Does a general formula exist?
I did find most of what I needed to answer these questions on the web. There is a world-beater site, the On-Line Encyclopedia of Integer Sequences (OEIS), founded in 1964 by N.J.A. Sloane, which contains thousands of numerical sequences, including double pronic numbers. The list begins as expected with 12 and 420, and the very next two are Pr(119) or 14280 and Pr(696) or 485112. So they are scarce and getting very large, but how do we find them?
I had reasoned that double pronics not only had to be pronic and twice another pronic, but they must be twice a triangular number as all pronics are. That meant our double pronics were four times a triangular number. I could write that fact in equation form.
Pr(k) = 4*T(n), or
k*(k+1) = 4*(n)*(n+1)/2
This equation can be made to fit the Pell form below with d = 2:
I had written in 2001, as Uncle Bob, an informal article about Pell equations which you might enjoy. My objective in that article was not to expose the mathematics, but rather the vast amount of history and culture that the subject embraces. Also, I had long ago studied the math topics involved in Pell solutions, namely continued fractions and convergents, and so I dug out a few texts. In them, and online, I found similar examples worked out, but not this example. Rather than drag the reader through it, I’ll cite resources which detail a similar solution below.
A Pythagorean Connection. At the OEIS someone had written that they were working on a paper that connected our double pronic sequence with Pythagorean triples {a, b, c}, the whole number measures of a right triangle’s sides, related by the well-known formula:

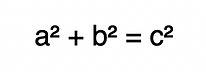
Our problem asks for all the triples {a, b, c}, but where a and b are consecutive wholes. So b is replaced by a + 1. Well since the area of right triangles is half the product of the legs, or in this case 0.5a*(a+1), the connection with the pronic a*(a+1) is evidenced.
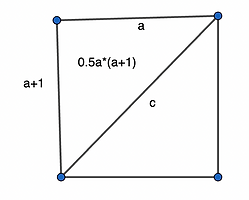

Let’s see further how Pythagoras connects to pronics. Twelve (3*4) is a double pronic, and {3, 4, 5} are the sides of a right triangle with area 6. The area of the rectangle encasing the triangle is 12. Next, we have the pronic double 420 (20*21), and {20, 21, 29} is the associated right triangle. The areas of triangle and rectangle are 210 and 420 square units, and note that a and b are consecutive.
The formula which solves for these triples in general is found through a Pell equation as well. We will skip the math details, but the reader is invited to consult Wolfram’s “Twin Pythagorean Triple” and the other resources, of course. Quite surprisingly, the solutions to the two problems are identical. Find the pronic double of a pronic number, and you have also found a Pythagorean triple {a, a + 1, c}, and vice versa, and the solutions are infinite in number.
For the benefit of those who can’t get enough of decimal digits, here are more of the pronic numbers which have pronic doubles:
{6, 210, 7140, 242556, 8239770, 279909630, 9508687656, 323015470680, 10973017315470, 372759573255306, 12662852473364940, 430164224521152660, 14612920781245825506, 496409142337836914550, 16863297918705209269200, …}.
The doubles begin {12, 420, 14280, 485112, 16479540, …} and on and on.
If these were the meat, then the Pythagorean connection was the gravy!
Next month, in the fourth and final leg of our journey, we explore connections among the pronic numbers and primes.
Sources
Sequence A029549, OEIS
Twin Pythagorean Triple, Wolfram
Convergents as Solutions for Pell’s Equation, Lubin
Convergents as solutions for Pell's equation, version: 2016-10-01)
Pell Equation and Convergents, Ben Lynn email
Adam
How to simplify this equation regarding pronic numbers for integer solutions, version: 2016-02-29
Pronic Triangular Numbers: for n >= 0, a(n+3) = 35*a(n+2) - 35*a(n+1) + a(n)
Mead, Bob. “An Equation Mis-Pelled”
Part Four
Pronics and Primes Awhirl
We conclude this journey with new ways to chart both the pronic and the prime numbers, and in the end we show how all the pronics could be displayed in one decimal number – if your calculator could but contain it!
In 1772 famed mathematician Leonhard Euler first noticed that the quadratic polynomial n^2 + n + 41, produced a string of 39 prime numbers when 1, 2, 3, … were substituted for n. This roused his interest because the vast set of primes appears to be distributed willy-nilly. The streak was broken when n reached 40 and produced a composite, non-prime number. Primes all the way until reaching 1,681 though.


In the 20th century Stan Ulam devised a doodle, like the one shown above, that dramatized this feature. On grid paper, he ran a squarish spiral counting up from a central number like 41, or even one, 11, or 17. After highlighting all the primes, he noticed a concentration of them in one diagonal – albeit, there were primes elsewhere, and the numbers in the diagonal were not all prime. The spiral around 41 had an impressive streak of 39 primes up and down that line.
My graph for a central 11 is at right. The prime streak ends at 121, 11 x 11 lower left, and also 143, 11 x 13 at the top.

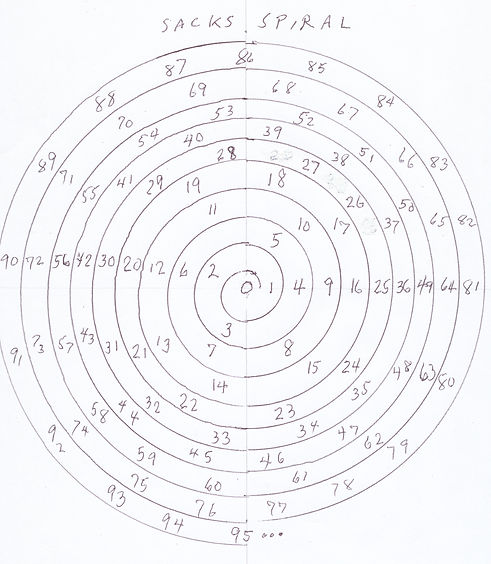
As noted in Part Two of this Journey, in 2003 software engineer Robert Sacks published a new way to chart the whole numbers. He placed them in a spiral running counterclockwise from zero in the center to each square number on the right, referred to as the easterly direction. So the entire one-dimensional whole number line is curled up in jellyroll fashion. In the sample at left, we see the pronic numbers running off in a westerly direction.
Since these prime-prone polynomials like Euler’s are merely our pronic formula, n*(n+1), adjusted up or down by a constant, when the primes are highlighted in the Sacks spiral (tiny black dots in the graph at right) the ones produced by this type of polynomial run in curves above and below the pronic, westward line. The traces of Euler’s polynomials for pronics plus or minus 11, 17, and 41 are easy to pick out above and below the pronic axis, and when the graph runs into the thousands as shown, these polynomials are shown to remain prime-rich.

In our technological world it’s important to know where the primes hang out. Hackers and legitimate researchers both can be saved time and effort with such knowledge. Since the security of our internet banking and online shopping depends on the relative unpredictability of the primes, discoveries such as these patterns may necessitate changes in the ways we currently are doing business.
We end this journey with a bit of calculator fun. If your machine displays nine digits you might see the beginnings of a display of all the pronic numbers in one decimal. We make use of what is known as a generating function. Calculate this number: two hundred million (200,000,000) divided by the cube of 999 (997,002,999) and see the start of the pronic sequence:
0.2006012020030042056072…
and so on until the digits run out of room and jumble together.
I had great fun leading this journey for you, and especially in learning more about these numbers than I knew at the start. I can’t wait until we trek again. -UB
Sources
Sacks spiral: Claudio Rocchini from Wikimedia Commons
Ulam Spiral: Bertrouf from Wikimedia Commons